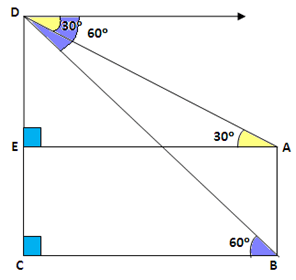
Given AB = 8 m be the height of the tall building
Hence CE = 8 m
Let the height of the multistoried building be CD = ‘h’ m
Therefore DE = CD – CE = (h – 8) m
Let BC = AE = x
In right ΔDCB, θ = 60°
$\Rightarrow \tan 60^{\cdot }=\dfrac {DC} {BC}$
$\Rightarrow \sqrt {3}=\dfrac {h} {x}$
$\therefore h=\sqrt {3}x\rightarrow \left( 1\right)$
In right ΔDEA, θ = 30°
$\begin{align*} & \Rightarrow \tan 30^{0}=\dfrac {DE} {EA}\\ & \Rightarrow \dfrac {1} {\sqrt {3}}=\dfrac {h-8} {x}\\ & \Rightarrow x\Rightarrow \sqrt {3}\left( h-8\right) \end{align*}$
$\begin{align*} & \Rightarrow \dfrac {h} {\sqrt {3}}=\sqrt {3}\left( h-8\right) \\ & \Rightarrow h=3\left( n-8\right) \\ & \Rightarrow h=3h-24\\ & \Rightarrow 2n=24\\ & \therefore h=12\end{align*}$
Thus the height of the multistoried building is 12 m