Total surface area of cylinder

Question

Radius_3.5
When sphere is placed in cylinder jar the water just cover the sphere

Answer 1

Total surface area of cylinder

Suppose a cylinder of radius r and height h. The total surface area (TSA) involves the area of the circular top and base, as well as the curved surface area (CSA).

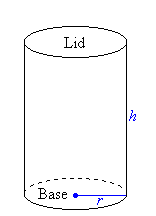
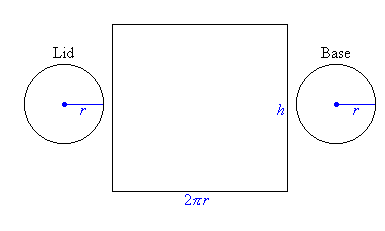
Now, the length of the rectangle
= Perimeter of the base
= 2πr

The Width of the rectangle
= Heigh of the Cylinder
= h

∴ TSA = Area of the Lid + Area of the Base + Curved Surface Area
= πr^{2 +} πr^{2 +} 2πrh
= 2πr2 + 2πrh
= 2πr (r+h)

The total surface area (TSA) of a cylinder with radius r and height h is given by

2πr (r+h)

The depth of water in the can before the sphere was put.

Volume of the can up to the length sphere is placed – Volume of the sphere = Volume of the can up to the depth of water that was in the can before the sphere was placed inside

πr²h – (4/3)πr³ =πr²H, where ‘h’ is the height of the can up to sphere is placed i.e. 2r = 2*3.5 = 7; r = 3.5 and H = depth of the water in the can before the sphere was put in (to find)

Now dividing both sides of the above equation by πr²
h – (4/3)r = H
=> 7 – (4/3)*3.5 = H
=> 7/3 = H

So 7/3 cm is the answer

(Source: mathsteacher, sscexamforum)